
第2回「よって」と「そこで」の違い
こんにちは。モノグサでソフトウェアエンジニアをしている宮坂です。
第1回 に引き続き、数学のコンテンツ制作の中でよく出てくる事例を取り上げて、数学教材ライティングのアンチパターン紹介をしましょう。
ベテランの方にはつまらないかもしれませんが、数学教材のライティングや編集を最近始めた方には、きっと参考になると思います。
「よって」という言葉
今回は、数学の解答でよく出てくる「よって」という言葉について考えましょう。
たとえば、このような問題があるとします。 (答えは「できる」です。)
長さが $${10}$$ である針金を直角に折り曲げて,両端に糸を張り,下の図のような直角三角形を作る。
このとき,面積が $${12}$$ である直角三角形を作ることはできるでしょうか。
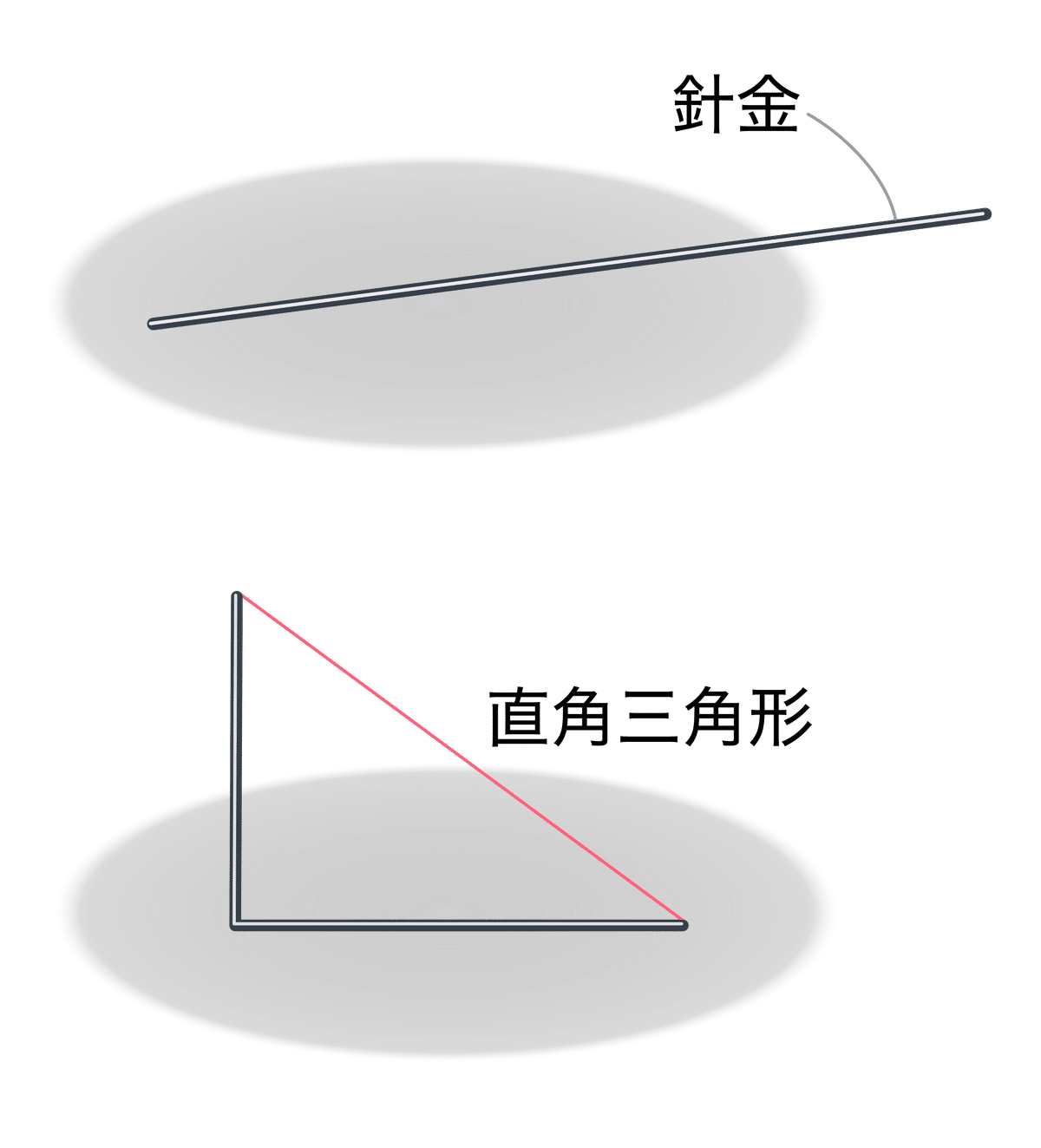
この問題の解答を書くとして、次の文の空欄に、どんな言葉を入れるでしょうか?
直角三角形の底辺を $${x}$$ とする。
長さが $${10}$$ の針金を折り曲げて作るので,直角三角形の高さは
$${10−x}$$
である。【 A 】,三角形の面積は
$${\displaystyle\frac{1}{2}x(10−x)}$$
となる。
【 B 】,方程式
$${\displaystyle\frac{1}{2}x(10−x)=12}$$
を考えると,
$${x(10−x)=24}$$
$${10x−x²=24}$$
$${x²−10x+24=0}$$
$${(x−4)(x−6)=0}$$
より,この解は
$${x=4,6}$$
である。
【 C 】,底辺を $${4}$$ とすると,高さは $${6}$$ なので,面積は
$${\displaystyle\frac{1}{2} \times 4 \times 6}$$
より,$${12}$$ となる。
同様に,底辺を $${6}$$ とすると,高さは $${4}$$ なので,面積は
$${\displaystyle\frac{1}{2} \times 6 \times 4}$$
より,$${12}$$ となる。
【 D 】,面積が $${12}$$ である直角三角形を作ることは できる 。(答)
空欄は、四つあります。
特に、今回のテーマである「よって」を入れてもよいかどうかを検討してみましょう。
「よって」 ―― 根拠から導かれる結論
まず、A は「よって」でよいでしょう。
直角三角形の底辺を $${x}$$ とする。
長さが $${10}$$ の針金を折り曲げて作るので,直角三角形の高さは
$${10−x}$$
である。【 A 】,三角形の面積は
$${\displaystyle\frac{1}{2}x(10−x)}$$
となる。
「よって」という言葉を使うのは、何か根拠になることを述べたあとで、そこから導かれる結論を述べるときです。
A は、まさにそういう場面ですよね。
実際、ここでは、
「底辺が $${x}$$ 」,「高さが $${10−x}$$ 」
ということを根拠として、
面積が $${\displaystyle\frac{1}{2}x(10−x)}$$ になる
という結論を導いています。
こういうときには「よって」を使えばよく、文章はこうなります。
直角三角形の底辺を $${x}$$ とする。
長さが $${10}$$ の針金を折り曲げて作るので,直角三角形の高さは
$${10−x}$$
である。【よって】,三角形の面積は
$${\displaystyle\frac{1}{2}x(10−x)}$$
となる。
また、同じ意味の言葉で、「これより」とか「ゆえに」などを入れてもよいですね。
別の観点からの言い換え
A には、「つまり」とか「すなわち」を入れる人もいるかもしれません。
意味は少し変わりますが、これでもよいですね。
これらは、前に述べたことを、わかりやすく言い換えて、別の観点から言い直すときに使う言葉です。
この場面では、前段で
「底辺が $${x}$$ で高さが $${10−x}$$」
ということを述べました。それを、私達の関心事である面積の観点でとらえ直して
「面積は $${\displaystyle\frac{1}{2}x(10−x)}$$ となる」
と言い換えるのですね。
ただし、「つまり」とか「すなわち」のような言葉は、論理的な言い換え、つまり必要十分条件のときにのみ使うという人もいるでしょう。
その場合は、A の場面では使えないということになります。
論理については、やや踏み込んだ話になりますが、少しだけ説明しましょう。
ここでは
底辺が $${x}$$ で高さが $${10−x}$$ ⇒ 面積が $${\displaystyle\frac{1}{2}x(10−x)}$$
という順向きの論理は正しく、一方で
底辺が $${x}$$ で高さが $${10−x}$$ ⇐ 面積が $${\displaystyle\frac{1}{2}x(10−x)}$$
という逆向きの論理は成立しません。
そのため、論理的に等価な言い換えをしているとはいえないのですね。
それで、必要十分条件というニュアンスのある「つまり」や「すなわち」を入れることには、抵抗がある人もいそうです。
もっともな考えだとは思うのですが、私は「あくまで面積に注目しているから」という理解で、許容して良いんじゃないかと思っています。
「そこで」 ―― 得た結果をもとにした行動
次に、Bはどうでしょうか。
私は「そこで」にすると思います。
よって,三角形の面積は
$${\displaystyle\frac{1}{2}x(10−x)}$$
となる。
【そこで】,方程式
$${\displaystyle\frac{1}{2}x(10−x)=12}$$
を考えると,
(略)
より,この解は
$${x=4,6}$$
である。
大切なのは、この場面では「よって」は使えないということです。
その理由は二つあります。
一つは、直前に「よって」があるので、たたみかけるような口調になってしまい、意図しないニュアンスが出るからというものです。
しかし、これは同じ「よって」を避けて、「これより」とか「ゆえに」のような同じ意味の言葉におき換えれば回避できます。
もう一つの理由のほうが重要です。
数学的な事実と、人間の行為
こちらを見てください。先ほどの文を簡単に省略したものです。
三角形の面積は $${\displaystyle\frac{1}{2}x(10−x)}$$ となる。
【 B 】,方程式 $${\displaystyle\frac{1}{2}x(10−x)=12}$$ を考えると,その解は $${x=4,6}$$ である。
この B に「よって」を入れたら、どうなってしまうのでしょうか。
先程も確認したように、「よって」というのは、前に述べた根拠をもとにして、そこから導かれる結論を述べようとする場面で使うのですね。
では、仮にこの場面で「よって」を入れるとして、「導かれる結論」とは何なのでしょうか?
そのときの読み方の候補は二つあります。
一つは
「方程式 $${\displaystyle\frac{1}{2}x(10−x)=12}$$ を考える」
という読み方です。
もう一つは
「方程式の解は $${x=4,6}$$ である」
という読み方です。
しかし、いずれも実態とは合わないでしょう。
面積が $${\displaystyle\frac{1}{2}x(10−x)=12}$$ であるというのは、数学的な事実です。
しかし、それを受けて「方程式 $${\displaystyle\frac{1}{2}x(10−x)=12}$$ を考える」というのは、私達の行為にすぎません。
単に私達が意思をもって「そのような方程式を考える」ことにしたのであり、これは根拠から導かれる結論ではないからです。
こんな場面では、「よって」は使えません。
「そこで,方程式 ○○○ を考える。」とするのが良いでしょう。
三角形の面積は ○○○ となる。
【そこで】,方程式 ○○○ を考えると,この解は ○○○ である。
「ここで」 ―― 導かれるのではない事実
では、次の C と D はどうでしょうか。
方程式
$${\displaystyle\frac{1}{2}x(10−x)=12}$$
を考えると,(略)この解は
$${x=4,6}$$
である。
【 C 】,底辺を $${4}$$ とすると,高さは $${6}$$ なので,面積は
$${\displaystyle\frac{1}{2} \times 4 \times 6}$$
より,$${12}$$ となる。(略)
【 D 】,面積が $${12}$$ である直角三角形を作ることは できる 。(答)
まず、明らかに「よって」が使える空欄がありますよね。
D のことです。
この D では、これまでの議論で分かったことを根拠にして、「作ることはできる」という結論を述べようとしているからです。
このように根拠から結論を導くときには、「よって」を使いましょう。
また、その他にも「ゆえに」、「これらから」、「以上より」、「したがって」のようなものを入れても大丈夫です。いずれも、最後の結論を述べる前に使う、同じ意味の言葉ですね。
それでは、C のほうはどうでしょうか。
私は「ここで」を入れると思います。
方程式
$${\displaystyle\frac{1}{2}x(10−x)=12}$$
を考えると,(略)この解は
$${x=4,6}$$
である。
【ここで】,底辺を $${4}$$ とすると,高さは $${6}$$ なので,面積は
$${\displaystyle\frac{1}{2} \times 4 \times 6}$$
より,$${12}$$ となる。(略)
【よって】,面積が $${12}$$ である直角三角形を作ることは できる 。(答)
「ここで」というのは、今までに述べたことから導かれる のではない 事実を、新しく述べようとするときの言葉です。
日常の会話でいえば、「そういえば」とか「ちなみに」といった言葉と同じ意味ですね。 話の中で連想したり、関連して思いついたりした、新しい話を初めるときの言葉です。
数学では、「そういえば」などは使いませんが、「ここで」の他にも「ところで」や「いま」といった言葉なら使うことがあります。これも、だいたい同じ意味です。
根拠のように言ってしまうとまずい
なぜ C には「よって」が入らないのか、もう少し説明しましょう。
この前に述べている
「方程式 $${\displaystyle\frac{1}{2}x(10−x)=12}$$ の解が $${x=4,6}$$ である」
というのは、考察してわかったことです。
一方で、これから書こうとしている
「底辺を $${4}$$ とすると,面積は $${12}$$ になる」
というのは、$${4}$$ が方程式の解だから言っているのではありません。
あらためて、実際に面積の公式で計算して求めているのです。
数学では、このようなものを「解の吟味」といいますね。
文章題では、方程式を解いて出てきた解を、ただちに信用することができません。
本当に文章題の答えであるかを確認するために、問題文にあてはめて計算してみるのです。 それが「解の吟味」です。
ここでいえば、本当に「直角三角形の面積が $${12}$$ になる」かどうかを確かめるために、実際に面積の公式にあてはめているのですね。
もし、仮に「ここで」ではなく「よって」を使ってしまうと、その前に述べた方程式の解を根拠としていることになってしまいます。
それでは、解の吟味とはいえません。あくまで、方程式の解を信用せずに、ゼロから確認してみせる必要があるのですね。
そんなときには、関連して思いついたことを述べる「ここで」のような言葉がぴったりです。
まとめと比較
ここで使った三つの言葉について、意味の違いを表でまとめると、このようになるでしょう。

最後に、全体をまとめると、このようになります。
直角三角形の底辺を $${x}$$ とする。
長さが $${10}$$ の針金を折り曲げて作るので,直角三角形の高さは
$${10−x}$$
である。【よって】,三角形の面積は
$${\displaystyle\frac{1}{2}x(10−x)}$$
となる。
【そこで】,方程式
$${\displaystyle\frac{1}{2}x(10−x)=12}$$
を考えると,
$${x(10−x)=24}$$
$${10x−x²=24}$$
$${x²−10x+24=0}$$
$${(x−4)(x−6)=0}$$
より,この解は
$${x=4,6}$$
である。
【ここで】,底辺を $${4}$$ とすると,高さは $${6}$$ なので,面積は
$${\displaystyle\frac{1}{2} \times 4 \times 6}$$
より,$${12}$$ となる。
同様に,底辺を $${6}$$ とすると,高さは $${4}$$ なので,面積は
$${\displaystyle\frac{1}{2} \times 4 \times 6}$$
より,$${12}$$ となる。
【よって】,面積が $${12}$$ である直角三角形を作ることは できる 。(答)
なお、この文では、空欄の B と C を逆にしてもよいでしょう。
つまり、B を「ここで」にして、C を「そこで」にするということです。
B を「そこで」にしたのは、この言葉は「〜を考える」という行為にかかっていると考えたからです。
しかし、その後の「解は〜〜である」という考察にかかっていると考えれば、B は「ここで」でもよいといえます。
同様に、C を「ここで」にしたのは、「面積は 12 となる」という考察にかかっていると考えたからです。
しかし、その前の「底辺を 4 にする」という行為にかかっていると考えれば、C は「そこで」でもよいですね。
「細部にこだわる」
モノグサ株式会社では「細部にこだわる」という行動指針を掲げています。
今回取り上げた「よって」や「そこで」のような言葉は、接続詞といって、これから述べようとする文がだいたいどんな文なのかを想像しやすくする働きがあります。
これから述べる文について、実際に述べる前に、およその意味を伝えることができるからです。
日常の会話では、何か提案をされたとき、「でもねえ…」という接続詞を言うだけで「私は賛同しない」という意図を伝えることさえできたりもしますよね。
接続詞は、一言で多くの意味を伝え、これから述べることをわかりやすくする言葉です。細かいですが、とても大切なものです。
Monoxerは、記憶事項を定着させるためのアプリです。
数学の処理を憶えたい人にとって、もしも説明の文章を読み解くことに時間や労力がかかっていたら、効率が悪くて仕方がありません。
スマートホンの小さいスペースで、少ない文字数で話を伝えるには、いつも一番ぴったりあてはまる接続詞を選ぶことが大事です。

